Constraint Based Analysis#
In this notebook, we are going to discuss some basics of CBA from their mathematical, theoretical and biological perspective.
Overflow metabolism is caused by two growth‑limiting constraints#
Literature
Overflow metabolism in Escherichia coli results from efficient proteome allocation.
The authors assume that the yield of energy per carbon molecule is higher for respiration than for fermentation: \(n{_r} > n{_f}\), but that fermentation is more proteome-efficient: \(\epsilon{_f} > \epsilon{_r}\).
Thermodynamically infeasible loops#
Quote from [8]
Quote!
One of the limitations of constraint-based genome-scale models is that the mass balance constraints only describe the net accumulation or consumption of metabolites, without restricting the individual reaction fluxes […] there can be cycles which do not consume or produce any metabolite. Therefore, the overall thermodynamic driving force of these cycles are zero, implying that no net flux can flow around this cycle [9].
The authors had a 4-side approach to identify such cycles: they turned off all the nutrient uptakes to the cell and used FVA which maximizes and minimizes each of the reaction fluxes subject to mass balance constraints. Fluxes reaching either the lower bound or upper bound were defined as unbounded reactions and were grouped together as a linear combination of the null basis (lumped) of their stoichiometric matrix. To eliminate the cycles, they:
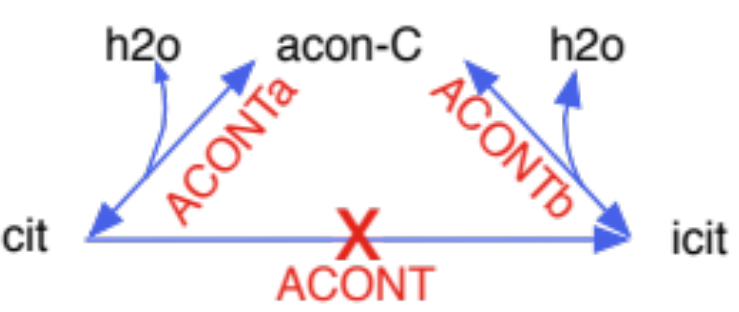
removed duplicate reactions: same reaction occurs both as reversible and irreversible
turned off lumped reaction: a model may include all steps of a process but also a lumped reaction of it:
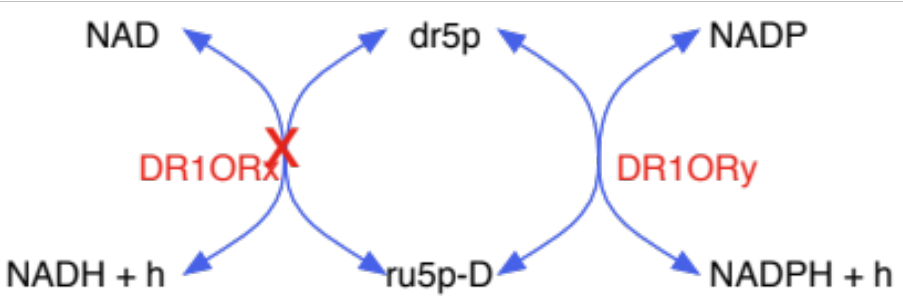
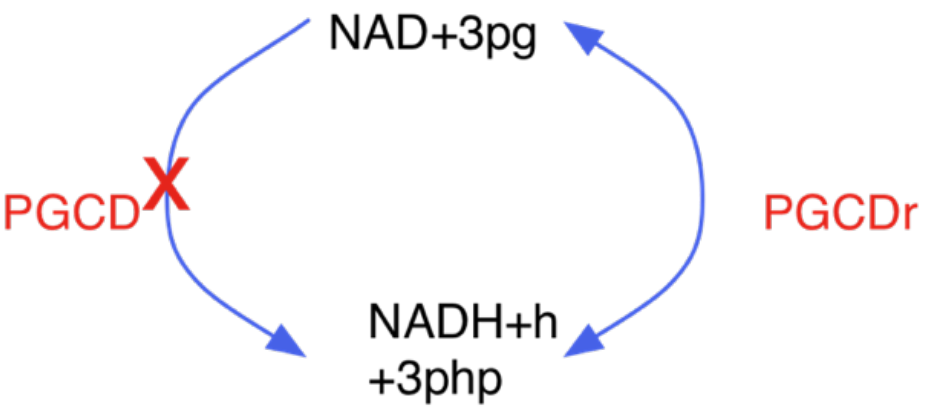
selectively turned reactions on/off based on available cofactor specificity information: the same biochemical conversion is carried out by different cofactors in the model, while in reality strain would use only one cofactor:
Applying random flux sampling to boundary reactions, we obtained probability distributions over metabolite exchange fluxes.
These probability distributions give an overview of the growth-supporting flux space, but they cannot be directly decomposed to the elementary metabolite conversions provided by pathways.
The issue here is that even in the smallest model, e_coli_core, none of the samples returned included CO2 uptake, which was feasible in the model and part of several pathways.
By sampling fluxes separately for each MP, we may find further uptake fluxes and that sampling could complement pathway analysis by allowing detailed analysis of individual pathways’ flux spaces.
Unbiased methods#
Minimal pathways#
Dictionary#
homogeneous constraint -> right-han-side is zero